Spinne Thekla möchte möglichst viele verschiedene Netze bauen.
Deshalb notiert sie sich die Struktur jedes ihrer Netze, und zwar so:

Sie nummeriert die Endpunkte des Netzes mit 1, 2, usw.
Die Struktur notiert sie dann in einem Raster,
das so viele Zeilen und Spalten hat wie das Netz Endpunkte hat.
Dann kreuzt sie die Felder im Raster nach dieser Regel an:

Wenn es einen Faden gibt, der von Endpunkt A zu Endpunkt B führt,
kreuzt sie das Feld in Spalte A und Zeile B an.

Beachte, dass Thekla für jeden Faden zwei Kreuze macht:
Ein Faden von Endpunkt A zu Endpunkt B führt auch von Endpunkt B zu Endpunkt A.

Hier siehst du ein Netz und wie Thekla seine Struktur notiert hat.

Thekla baut nun dieses Netz:

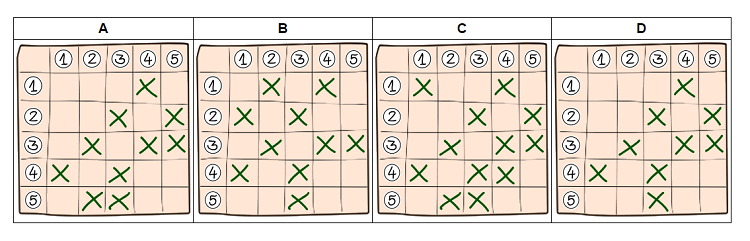
Wie notiert Thekla die Struktur dieses Netzes?

Antwort A ist richtig:

Im Raster von Antwort A sind alle Felder gemäß der Regel angekreuzt:
Von Endpunkt 1 führt genau ein Faden, und zwar zu Endpunkt 4.
Von Endpunkt 2 führen genau zwei Fäden, und zwar zu den Endpunkten 3 und 5.
Von Endpunkt 3 führen genau drei Fäden, und zwar zu den Endpunkten 2, 4 und 5.
Von Endpunkt 4 führen genau zwei Fäden, und zwar zu den Endpunkten 1 und 3.
Von Endpunkt 5 führen ebenfalls genau zwei Fäden, und zwar zu den Endpunkten 2 und 3.

Die Raster der anderen Antworten unterscheiden sich von dem von Antwort A. Deshalb sind dort nicht alle Felder gemäß der Regel angekreuzt:


Antwort B: Hier sind Felder für einen Faden von Endpunkt 1 nach Endpunkt 2 (und umgekehrt) angekreuzt, den es in Theklas Netz aber nicht gibt. Dafür wurden die Felder für den Faden von Endpunkt 2 nach Endpunkt 5 nicht angekreuzt.
Antwort C: In diesem Raster sind Felder in der Diagonale von links oben nach rechts unten angekreuzt. Das kann es aber nur geben, wenn ein Faden an einem Endpunkt eine Schleife bildet, also zum selben Endpunkt zurückführt. Eine solche Schleife gibt es in Theklas Netz nicht, erst recht nicht bei den Endpunkten 1 und 4, wie die Kreuze in Antwort C anzeigen.
Antwort D: Die Kreuze im Raster sollten ein Muster bilden, das symmetrisch ist zur Diagonale von links oben nach rechts unten: Jeder Faden von Endpunkt A zu B führt auch von B zu A, und deshalb gibt es für jedes Kreuz in Spalte A und Zeile B auch eines in Spalte B und Zeile A. In diesem Raster gibt es ein Kreuz in Spalte 2 und Zeile 5, aber keines in Zeile 5 und Spalte 2.

Das Spinnennetz kann als Graph betrachtet werden, ein Konzept, das häufig in der Informatik verwendet wird.

Ein Graph besteht aus Knoten (den Endpunkten des Netzes) und Kanten (den Fäden zwischen den Endpunkten). Graphen werden zum Beispiel auch verwendet, um Objekte und die Beziehungen zwischen Objekten darzustellen. Ein Diagramm könnte beispielsweise Personen zeigen, die in sozialen Medien befreundet sind, oder Flüge zwischen Ländern.

In dieser Aufgabe wird gezeigt wie man die Struktur eines Spinnennetzes in einem Raster speichern kann. Gewisse Eigenschaften, wie zum Beispiel das genaue Aussehen des Netzes, gehen dabei verloren. In vielen Fällen ist man aber nicht an den genauen geometrischen Eigenschaften des Graphen interessiert sondern nur an seiner Struktur. Gewisse Eigenschaften des Graphen bleiben erhalten: Existiert eine bestimmte Kante? Wie viele Kanten sind mit einem bestimmten Knoten verbunden?



Die vorgestellte Möglichkeit ist nur eine von vielen Möglichkeiten die Struktur eines Netzes festzuhalten. Die Methode ist nicht sehr sparsam, denn es werden für jede Verbindung beide Richtungen gespeichert, was nicht notwendig wäre und auch die freien Diagonalenfelder wären gar nicht notwendig. Dafür weist dieses Verfahren den Vorteil auf, dass Darstellungsfehler teilweise erkannt werden können. Antwort C und Antwort D konnten zum Beispiel als falsch erkannt werden ohne auf das Netz Bezug zu nehmen.

Die vorgestellte Darstellungsform wird Adjazenz-Matrix genannt.